MarbleAdder
(→Die Maschine) |
(→Rechnet Selbst) |
||
| Line 271: | Line 271: | ||
==Rechnet Selbst== | ==Rechnet Selbst== | ||
| + | |||
| + | Zwei Zahlen bitte! | ||
| + | |||
| + | 7 | ||
| + | |||
| + | 10 | ||
| + | |||
| + | Wandeln wir das mal in binär | ||
| + | |||
| + | 7 ergibt 0111 | ||
| + | |||
| + | 10 ergibt 1010 | ||
| + | |||
| + | Das geben wir jetzt ein (dies video ist noch vom nicht fertigen Modell, ohne eingangs Tore und ohne resultat Anzeige). | ||
| + | |||
| + | {{#ev:youtube|wDm7Nk6CEgk}} | ||
| + | |||
| + | Resultat ist 10001, also 17 | ||
| + | |||
| + | |||
| + | <!-- | ||
| + | hier könnte man 100 videos machen für alle möglichen rechnungen | ||
| + | 0000+0000=0000 | ||
| + | 0000+0001=0001 | ||
| + | 0000+0010=0010 | ||
| + | ... | ||
| + | 0000+1111=1111 | ||
| + | etc... | ||
| + | |||
| + | --> | ||
=Presentation done to the public= | =Presentation done to the public= | ||
Revision as of 15:56, 29 November 2011
For those finding this page "oh, not another one!" well I want to document here:
- how we built the thing
- how we presented the thing
Please dont link here until dust is settled.
First part: in german!
Contents |
Presentation done to the Kids
Binäre Zahlen und Rechnen
Intro
Der syn2cat Hackerspace aus Luxemburg will hier ein wenig erklären wie moderne Computer mit Zahlen umgehen.
Binär
Das erste Problem das sich ergibt ist dass Computer mit Strom funktionieren, und es gibt entweder Strom oder keinen Strom. Einen halb geschlossenen Schalter kennt der Computer nicht. Wenn wir jetzt sagen dass kein Strom der Zahl 0 entspricht und der eingeschalteten Strom der Zahl 1, was machen wir für die 2?
Da können wir uns an einem ähnlichen Problem in useren normalen Zahlenwelt inspirieren. Wir zählen bis 9, und danach wissen wir nicht mehr weiter. Es gibt keine Ziffer nach der 9. Um den nächsten Wert dar zu stellen schreiben wir dann 2 Stellen. Eine 1 und eine 0, und dann können wir weiter Zählen. Beim Computer wird die gleiche Technik angewandt, nur dass der Computer schon nach der 1 nicht mehr weiter weiß. Er kennt die Ziffer 2 nicht. Also für den nächsten Wert nimmt er dann 2 Stellen und schreibt eine 1 und eine 0. An der niedrigste Stelle wird dann weiter gezählt aber man erreicht sech schnell wieder die 1. Also muss jetzt di nächste Stelle erhöht werden auf 2, welche es nicht gibt, also auch noch die dritte Stelle erhöhen.
| Wir zählen so | der computer so |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 1 0 |
| 3 | 1 1 |
| 4 | 1 0 0 |
Dies nennt man das binäre Zahlensystem
Wie stellt der computer also Zahlen dar. Dafür können wir uns eine einfache Gedankenstütze bauen. Man nimmt Karten mit den jeweiligen werten 1, 2, 4, 8 und legt sie in die folgende Reihenfolge ab:
| 8 | 4 | 2 | 1 |
Die Reihenfolge ist wichtig und darf nicht verändert werden. Welche karten muss man nun zeigen um in der Summe eine 9 zu erhalten?
| 8 | _ | _ | 1 |
Der Computer behält sich dies Information indem er speichert an welcher Stelle eine Karte umgedreht ist und schreibt dort eine 1, wir erhalten also
1 0 0 1
Das Gleiche für eine 10
| 8 | _ | 2 | _ |
Das ergibt in der binären Computer Sprache:
1 0 1 0
Und nun schauen wir was die Summe beider Zahlen ergibt 9+10=19... hmm, das können wir mit unseren Karten nicht mehr darstellen, drum wird eine neue Karte eingeführt. Aber welchen Wert? Mit den aktuellen Karten kann man Werte bis 15 darstellen (1+2+4+8=15) also bekommt die nächste Karte den wert 16. Diese Karte stellen wir ganz links.
| 16 | _ | _ | 2 | 1 |
Der Computer schreibt also 19 so:
1 0 0 1 1
Wir haben nun gesehen wie unsere Rechnung im Computer aussieht
| _ 1 0 0 1 | 9 + |
| _ 1 0 1 0 | 10 |
| 1 0 0 1 1 | 19 |
Schaut man sich die binäre Seite genau an, erkennt man eine art Tafelrechnung, und die kann man auch errechnen.
1+0=1
0+1=1
0+0=0
1+1=2 hmm, nicht wirklich, der Computer kennt keine 2. Also verfährt er genau so wie wir wenn wir bei einer 9 was hinzu rechnen: wir benutzen einen Übertrag. Beim Computer besteht der Übertrag aus 1, und wir schreiben eine 0.
1+1=Übertrag 1, schreiben 0
Ein spezial Fall gibt es wenn wir 1+1 rechnen aber es auch schon einen Übertrag von der vorherigen Stelle gibt. Dann ist die Rechnung 1+1+1=11 (binär). Dies kann man aber in Einzelschritte aufteilen. Zuerst rechnen wir wie vorher die Operanden zusammen: 1+1=10. Dann wird noch der Übertrag hinzu gerechnet: 0+1=1
In der Elektronik wird zur Vereinfachung immer der Übertrag hinzu gerechnet, auch wenn der meistens 0 ist und man also den Rechenschritt überspringen könnte.
Logik
Wie kommt man nun von der binären Tafelrechnung zur logik? Wenn man die Operationen die wir bei der Tafelrechnung gemacht hat einzel sieht stellt man fest dass wir 2 Funktionen brauchen.
- Eine addition für die standard rechnung, dies ergibt den Wert den wir unter den Strich schreiben. Also:
| wert A | wert B | Resultat |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Die letzte Zeile ist die Addition 1+1= scheibe 0, Übertrag 1
Wir brauchen also eine Schaltung welche 1 liefert nur wenn genau ein Wert 1 ist, aber nicht wenn beide 1 sind. In der Logik bezichnet man solch eine Funktion ein exklusiv-oder Gatter. Kurz XOR.
Dies kann man folgendermassen in mechanik implementieren. Die beiden Eingangswerte werden links eingegeben indem man die Stangen hinen drückt. Bitte beachte in dem Foto die Stange die seitlich verläuft und mit XOR markiert ist.
 Nur wenn man einen der beiden Eingänge drückt bewegt sich der XOR Hebel. Wenn man beide drückt passiert hingegen nichts. Dies ist also ein mechanisches XOR Gatter.
Nur wenn man einen der beiden Eingänge drückt bewegt sich der XOR Hebel. Wenn man beide drückt passiert hingegen nichts. Dies ist also ein mechanisches XOR Gatter.
Auf dem Foto sieht man aber auch noch eine Stange die geradeaus weiter geht und mit AND markiert ist. Dies ist das und-Gatter und kümmert sich um den Übertrag.
| wert A | wert B | Resultat |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Der Übertrag wird nur benötigt wenn beide Werte 1 sind, sonst nicht. Genau so verhält sich dei AND Stange. Sie bewegt sich nur wenn beide Eingangshebel gedrückt werden.
Diese Kombination aus einem XOR und einem AND Gatter nettn man Halbaddierer (auf Englisch half-adder).
Damit kann man bis 2 Rechnen, also bis binär 10. Der XOR Ausgang ist das niederwertige Bit, der AND Augang das höherwertige Bit. Wir können also folgende Rechnungen machen:
| wert A | wert B | AND | XOR | binär | dezimal |
| 0 | 0 | 0 | 0 | 00 | 0 |
| 0 | 1 | 0 | 1 | 01 | 1 |
| 1 | 0 | 0 | 1 | 01 | 1 |
| 1 | 1 | 1 | 0 | 10 | 2 |
Diese kleine Lego mechanik ist also eine primitive rechenmachine die 2 Bits zusammenrechnen kann. Um jetzt grössere Zahlen zu berechnen braucht man nur mehrere solche halb-Addierer zusammen zu schliessen.
Um die Mechanik skalierbar zu machen wurde das Ganze in Kupfer zusammen gelötet und die Hebel werden von Murmeln gedrückt. Die Resultate sind auch wiederum Murmeln welche dann die Hebel im nächsten Halbaddierer betätigen. Hier wird das anhand des allerersten prototyps gezeigt (englisch)
Diese logik Bausteine kann man auch schematisch darstellen. Hier ein AND und ein XOR mit ihren jeweiligen Ein- und Ausgängen.
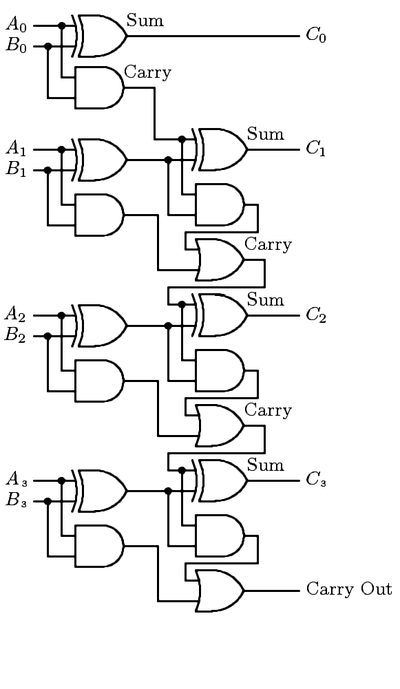
Ein Halbaddierer erlaubt uns bei der binären Tafelrechnung die erste Stelle (A0+B0) zu berechen und gibt ein Resultat (C0) und ein Übertrag (carry) aus. Für die zweite Stelle (A1+B1) benutzen wir auch einen Halbaddierer. Dieser ergibt auch ein Resultat und ein Übertrag. Das Resultat muss aber auch noch mit dem vorherigen Übertrag zusammerechnen. Dazu benutzen wir einfach noch einen Halbaddierer. Dann erhält man das endgültige Resultat für diese Stelle (C1).
In folgendem Schema sieht man die Reihenfolge der einzelnen Bausteine.
Da ist auch ein neuer Baustein aufgetaucht. Sieht fast so aus wie ein XOR, aber es hehlt der zweite Strich. Dies ist ein normales ODER, was nicht viel mehr ist als eine einfache Zusammenschaltung der 2 Leitungen.
Mechanik
Hier wird der Halbaddierer aufgebaut. Das logik Gestänge ist schon eingebaut inklusie der Hebel welche betätigt werden. Grad hier wird der zweite Fangkorb für die eingabe-Murmeln angebracht.
Der fertig aufgebaute Haldaddierer ist hier eingebaut mit einem Zweiten um einen kompletten Fulladder zu erhalten. Im Hintergrund steht noch ein Fulladder dessen carry Ausgang über den Looping zum Fulladder im Vordergrund verbunden ist.
Nahaufnahme:
Die Maschine
Wie man vorher schon sieht kann man die Halbaddierer einfach hintereinander schalten um so eine grössere bitzahl zu addieren. Für unseren Addierer haben wir 7 Stück zusammen geschaltet. Dies erlaubt uns zwei Zahlen zu je 4 Bit zusammen zu rechnen.
Die Ausgabe hat 1 Bit mehr, dieses wird "carry out" genannt und kann dazu dienen grössere Zahlen zu berechen. In userem Fall ist es einfach nur das höchstwertige Bit des Resultates und hat eine wertigkeit von 16.
Die einzelnen Ausgänge werden über Spiralen nach unten geführt damit man dort das Resultat praktisch ablesen kann. Die beiden Eingänge A und B werden Bit pro Bit in die jeweiligen Addierer eingelegt. Also rechts aussen die 4 wertigen Bits der beiden Operanden und ganz links die niedrigwertigen Bits.
Also:
A B A3 A2 A1 A0 B3 B2 B1 B0
1001+1010 ----> 1 0 0 1 1 0 1 0
|
|
V
A3 B3 A2 B2 A1 B1 A0 B0
1 1 0 0 0 1 1 0
Eine zusatz Murmel setzt das ganze Rechenwerk in Bewegung:
* laden der beiden Operanden in die Addierer
* der erste halbaddierer rechnet A0+B0 = 01
* der zweite rechnet A1+B1 = 01 |
* der dritte rechnet |_____ ____|
+
=1
resultat full adder 1: 01
* nummer vier: A2+B2=00 |
* nummer fünf: +-------->0<--+
resultat full adder 2: 00
* nummer sechs: A3+B3=10 |
* nummer sieben: +-->0<--+
full adder 3: 10
Eine andere rechnung mit video: 13+11
A B A3 A2 A1 A0 B3 B2 B1 B0
1101+1011 ----> 1 1 0 1 1 0 1 1
|
|
V
A3 B3 A2 B2 A1 B1 A0 B0
1 1 1 0 0 1 1 1
* der erste halbaddierer rechnet A0+B0 = 10
* der zweite rechnet A1+B1 = 01 |
* der dritte rechnet |_____ ____|
+
=10
resultat full adder 1: 10
* nummer vier: A2+B2=01 |
* nummer fünf: +------->10<--+
resultat full adder 2: 10
* nummer sechs: A3+B3=10 |
* nummer sieben: +-->1<--+
full adder 3: 11
Und wir erhalten 11 0 0 0
11000 binär ist 24
Und hier das video
Rechnet Selbst
Zwei Zahlen bitte!
7
10
Wandeln wir das mal in binär
7 ergibt 0111
10 ergibt 1010
Das geben wir jetzt ein (dies video ist noch vom nicht fertigen Modell, ohne eingangs Tore und ohne resultat Anzeige).
Resultat ist 10001, also 17